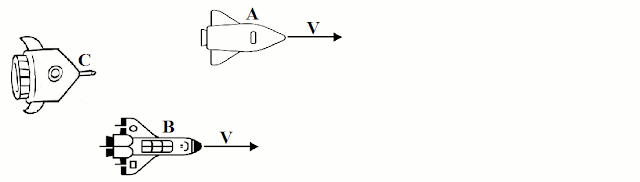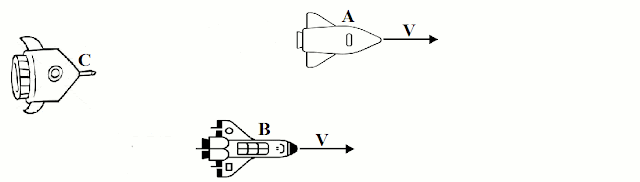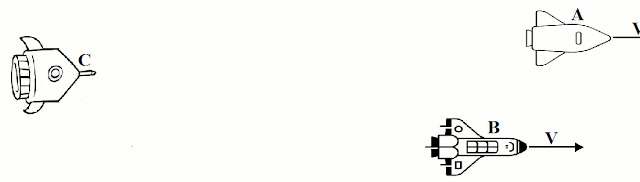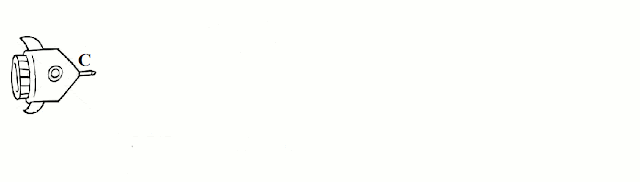
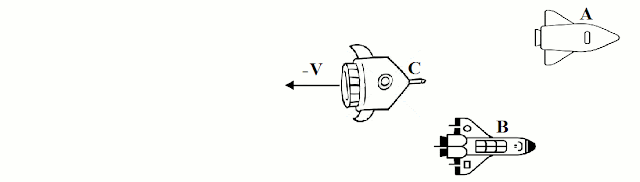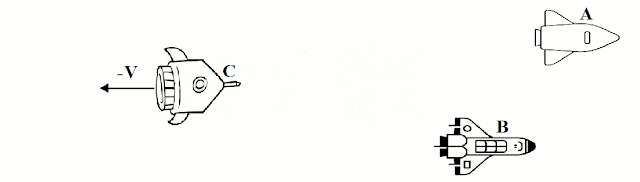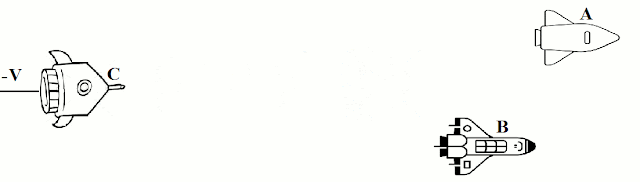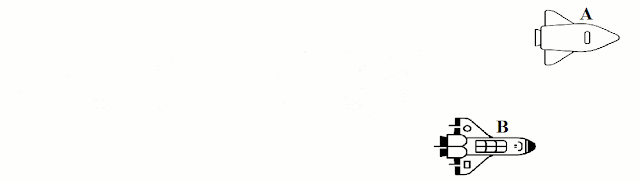
Os movimentos dependem do referencial a partir do qual são observados os corpos.
Imagine três naves espaciais, A, B, e C, com motores desligados, em movimento apenas por inércia. Para um observador na nave C, as naves A e B se afastam com a mesma velocidade v.
Já para um observador na nave A (ou B), a nave C é que se afasta com velocidade -v.
O mesmo observador na nave A acharia que a nave B está em repouso, já que sua posição não muda com o tempo em relação a sua nave.
Para um observador em uma quarta nave D, diria que a nave C tem velocidade v', enquanto A e B têm velocidades v''.
Essas animações são para mostrar que o movimento é relativo, ou seja, indica que ele é sempre medido por um observador em relação a um referencial (normalmente o referencial próprio, aquele que acompanha o corpo/observador). Um mesmo corpo pode ter seu movimento descrito por vários observadores diferentes, ou seja, relativo à vários referenciais distintos.
Galileu (1564-1642) ao estudar o movimento de corpos na superfície da Terra, tentou mostrar a equivalência entre os diferentes pontos de vista observados pelos que enxergavam o movimento de um corpo, ou seja, a relatividade do movimento.
Talvez essa questão nos pareça mais simples atualmente, mas foi uma das questões mais intrigantes para os filósofos naturais e cientistas durante muitos séculos. A Terra foi considerada por muito tempo o "centro do Universo" (Modelo Geocêntrico do Universo), isso porque só considerávamos os movimentos dos outros corpos celestes no Sistema Solar, e no próprio Universo, em relação à Terra, ou seja, víamos o universo apenas da perspectiva do nosso referencial próprio.
Galileu (1609) foi o primeiro a relatar o movimento de luas (satélites naturais) ao redor de Júpiter através de observações realizadas com uma luneta rudimentar desenvolvida por ele, mostrando que nem tudo girava em torno da Terra, e reforçava a ideia da relatividade do movimento.
Talvez essa questão nos pareça mais simples atualmente, mas foi uma das questões mais intrigantes para os filósofos naturais e cientistas durante muitos séculos. A Terra foi considerada por muito tempo o "centro do Universo" (Modelo Geocêntrico do Universo), isso porque só considerávamos os movimentos dos outros corpos celestes no Sistema Solar, e no próprio Universo, em relação à Terra, ou seja, víamos o universo apenas da perspectiva do nosso referencial próprio.
Galileu (1609) foi o primeiro a relatar o movimento de luas (satélites naturais) ao redor de Júpiter através de observações realizadas com uma luneta rudimentar desenvolvida por ele, mostrando que nem tudo girava em torno da Terra, e reforçava a ideia da relatividade do movimento.
Por questões ideológicas, religiosas e conservadoras, muitas pessoas foram mortas por discordarem dessa ideia (modelo geocêntrico) durante a idade média, tanto pela a Igreja Católica, quanto pela Igreja Católica Ortodoxa e protestantes (Calvinista, Luterana, Anglicana, Puritana). Por aí já podemos ver que essa NÃO É UMA SIMPLES QUESTÃO . O próprio Galileu foi preso por muitos anos, e só não foi condenado à morte por ter amizade com o Papa.
Velocidade relativa
Velocidade relativa
Representa a velocidade em que dois móveis se afastam, ou se aproximam, um em relação ao outro, na mesma reta que os liga. Seu módulo é sempre o mesmo, independentemente das suas velocidades medidas a partir de um referencial inercial R.
A determinação da velocidade relativa corresponde ao módulo da diferença vetorial das componentes das velocidades dos móveis na direção da reta que os liga.
Para se determinar a velocidade relativa vR entre dois móveis, existem duas situações que precisamos destacar:
1. Quando os móveis estão em movimento na mesma reta:
A determinação da velocidade relativa corresponde ao módulo da diferença vetorial das componentes das velocidades dos móveis na direção da reta que os liga.
Para se determinar a velocidade relativa vR entre dois móveis, existem duas situações que precisamos destacar:
1. Quando os móveis estão em movimento na mesma reta:
Imagine dois automóveis que se aproximam em sentidos opostos em um trecho retilíneo de uma estrada. As suas velocidades são medidas a partir de um referencial inercial R, fixo na estrada, onde o sentido para a direita é considerado positivo.
A velocidade relativa vR entre eles, é:
Para vetores na mesma direção, o que importa são as suas intensidades, que pode ser positiva ou negativa. Lembre-se, em uma mesma direção, vetores opostos devem ter intensidades opostas (sinais opostos):
Assim:
Ambos os motoristas em cada automóvel vêem um ao outro se aproximando com velocidade de 150kmh (velocidade relativa).
Agora, imagine um automóvel (A) que acabou de ultrapassar o outro (B) na estrada. O mais veloz segue na frente, se distanciando com o tempo. O da frente vê, através do retrovisor, que o outro vai ficando para trás com uma velocidade vR. O de trás vê o da frente se distanciando com a mesma velocidade vR .
Qual a velocidade relativa entre eles?
Percebe que se fizesse:
A velocidade relativa seria a mesma, já que ela corresponde ao módulo da diferença.
Caso você escolha um referencial R' que acompanhe um dos móveis (referencial próprio), a velocidade relativa representaria a velocidade do outro móvel medido a partir do referencial próprio.
Essa mudança de referencial é muito interessante para resolver problemas que envolvam aproximação e afastamento de móveis, com velocidades medidas a partir de um referencial R (fixo na estrada, por exemplo).
Para vetores na mesma direção, o que importa são as suas intensidades, que pode ser positiva ou negativa. Lembre-se, em uma mesma direção, vetores opostos devem ter intensidades opostas (sinais opostos):
Assim:
Ambos os motoristas em cada automóvel vêem um ao outro se aproximando com velocidade de 150kmh (velocidade relativa).
Agora, imagine um automóvel (A) que acabou de ultrapassar o outro (B) na estrada. O mais veloz segue na frente, se distanciando com o tempo. O da frente vê, através do retrovisor, que o outro vai ficando para trás com uma velocidade vR. O de trás vê o da frente se distanciando com a mesma velocidade vR .
Qual a velocidade relativa entre eles?
Percebe que se fizesse:
A velocidade relativa seria a mesma, já que ela corresponde ao módulo da diferença.
Caso você escolha um referencial R' que acompanhe um dos móveis (referencial próprio), a velocidade relativa representaria a velocidade do outro móvel medido a partir do referencial próprio.
Essa mudança de referencial é muito interessante para resolver problemas que envolvam aproximação e afastamento de móveis, com velocidades medidas a partir de um referencial R (fixo na estrada, por exemplo).
2. Quando os móveis estão em movimento em retas diferentes:
Imagine dois pequenos móveis, A e B, com velocidades vA e vB, respectivamente, medidas em relação a um referencial R :
Para se determinar a velocidade relativa entre eles (instantânea), precisamos projetar (ortogonalmente) as velocidades de cada um dos móveis sobre a reta que os separa. Mas vB já está nessa direção. Então, precisaremos determinar apenas a projeção de vA:
Por definição, o cateto adjacente (v'A) dividido pela hipotenusa (vA) corresponde ao seno do ângulo (60graus), no triângulo retângulo formado na projeção. Assim:
O problema se resume agora a:
Então:
Instantaneamente, a velocidade entre eles é nula. Se fôssemos calcular a velocidade relativa entre eles em outro instante t, teria outro valor e direção.
Vamos ver dois exemplos?
1. Uma motociclista anda com velocidade constante de 120km/h, no mesmo sentido que segue um automóvel com velocidade também constante, mas menor, de 90km/h, em um trecho retilíneo de uma estrada. As velocidades são relativas a um referencial R fixo na estrada.
a) Qual a velocidade relativa entre eles?
b) Sabendo que inicialmente a distância entre eles era de 2km, em quanto tempo a motocicleta alcançará o automóvel?
Resolução:
a) Como já estão na mesma reta, a velocidade relativa entre eles, é:
b) Para a motociclista (no seu referencial próprio), o automóvel se aproxima com velocidade de 30km/h. Como a distância d que os separa é de 2km, o tempo t para alcançar o automóvel, será:
Existe uma outra forma de se resolver problemas que envolvam aproximação e afastamento como este. Mas para isso, precisaríamos obter uma função horária da posição (ou espaço) para cada móvel (x(t) = x0+ v . t) , depois resolver o sistema de equação obtido. A velocidade relativa torna a resolução mais simples.
2. Dois automóveis, A e B, partem ao mesmo instante de um ponto, em direções perpendiculares, mantendo as velocidades constantes.
a) Qual a velocidade relativa entre eles?
b) Considerando que mantenham as velocidades sempre constantes, quanto tempo depois estarão distantes 1km?
Resolução:
a) Como as velocidades são constantes, após um certo tempo t, ambos terão percorrido uma distância 𝓁, e estarão distantes d:
A projeção das velocidade sobre a reta que separa os automóveis tem o mesmo valor em módulo, assim:
Logo,
v'A=36km/h (para cima é positivo)
v'B=-36km/h (para baixo é negativo)
Assim a velocidade relativa, é:
Percebe que, neste caso, a velocidade relativa é constante.
b) Quando imaginamos um referencial próprio em um dos automóveis, um vê o outro se afastar com uma velocidade de v=72km/h, na mesma direção; assim, quando d = 1km:
Não fique preocupado(a), grande parte das questões que nos deparamos sobre velocidade relativa os móveis já estão sobre uma mesma reta, ok?!
Vamos fazer um pequeno teste?
→Clique qui para fazer o teste.
Precisamos ainda conhecer uma importante grandeza física para que possamos continuar os nossos estudos, a aceleração. Talvez você já tenha estudado em outro momento, mas vamos revê-la?
→Clique qui para continuar.
O problema se resume agora a:
Então:
Vamos ver dois exemplos?
1. Uma motociclista anda com velocidade constante de 120km/h, no mesmo sentido que segue um automóvel com velocidade também constante, mas menor, de 90km/h, em um trecho retilíneo de uma estrada. As velocidades são relativas a um referencial R fixo na estrada.
a) Qual a velocidade relativa entre eles?
b) Sabendo que inicialmente a distância entre eles era de 2km, em quanto tempo a motocicleta alcançará o automóvel?
Resolução:
a) Como já estão na mesma reta, a velocidade relativa entre eles, é:
Existe uma outra forma de se resolver problemas que envolvam aproximação e afastamento como este. Mas para isso, precisaríamos obter uma função horária da posição (ou espaço) para cada móvel (x(t) = x0+ v . t) , depois resolver o sistema de equação obtido. A velocidade relativa torna a resolução mais simples.
2. Dois automóveis, A e B, partem ao mesmo instante de um ponto, em direções perpendiculares, mantendo as velocidades constantes.
a) Qual a velocidade relativa entre eles?
b) Considerando que mantenham as velocidades sempre constantes, quanto tempo depois estarão distantes 1km?
Resolução:
a) Como as velocidades são constantes, após um certo tempo t, ambos terão percorrido uma distância 𝓁, e estarão distantes d:
A projeção das velocidade sobre a reta que separa os automóveis tem o mesmo valor em módulo, assim:
v'A=36km/h (para cima é positivo)
v'B=-36km/h (para baixo é negativo)
Assim a velocidade relativa, é:
Não fique preocupado(a), grande parte das questões que nos deparamos sobre velocidade relativa os móveis já estão sobre uma mesma reta, ok?!
Vamos fazer um pequeno teste?
→Clique qui para fazer o teste.
Precisamos ainda conhecer uma importante grandeza física para que possamos continuar os nossos estudos, a aceleração. Talvez você já tenha estudado em outro momento, mas vamos revê-la?
→Clique qui para continuar.