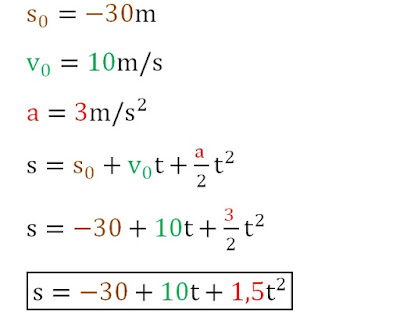É o movimento que apresenta aceleração constante, ou seja, a aceleração tem sempre a mesma intensidade e direção. Esse tipo de movimento é chamado de uniformemente variado (MUV).
A palavra "variado" pode ser substituída por "acelerado", se o módulo da velocidade aumenta com o tempo, ou "retardado", se o módulo da velocidade diminui com o tempo.
O MUV tem apenas aceleração tangencial (atg), já que a aceleração não muda de direção (é constante); e a aceleração centrípeta (acp) é nula:
Muitas vezes é chamado de movimento retilíneo uniformemente variado, mas isso é redundante, já que a velocidade não muda de direção, porque a aceleração (que é constante) muda apenas a sua intensidade; logo, só pode ser um movimento retilíneo.
No sistema internacional de Unidades (S.I), a unidade para a aceleração é o metro por segundo quadrado (m/s²), que é o mesmo que:
Uma outra implicação, é que o móvel sofre variações de velocidade iguais, em intervalos de tempo iguais.
A palavra "variado" pode ser substituída por "acelerado", se o módulo da velocidade aumenta com o tempo, ou "retardado", se o módulo da velocidade diminui com o tempo.
O MUV tem apenas aceleração tangencial (atg), já que a aceleração não muda de direção (é constante); e a aceleração centrípeta (acp) é nula:
Muitas vezes é chamado de movimento retilíneo uniformemente variado, mas isso é redundante, já que a velocidade não muda de direção, porque a aceleração (que é constante) muda apenas a sua intensidade; logo, só pode ser um movimento retilíneo.
No sistema internacional de Unidades (S.I), a unidade para a aceleração é o metro por segundo quadrado (m/s²), que é o mesmo que:
Uma outra implicação, é que o móvel sofre variações de velocidade iguais, em intervalos de tempo iguais.
Por exemplo, se um móvel parte do repouso com aceleração (tangencial) constante de módulo a=6m/s², sua velocidade aumentará 6m/s a cada segundo, ou 12m/s a cada 2s:
O lançamento vertical
e a queda livre
são exemplos de movimentos uniformemente variados.
Nas proximidades da superfície da Terra, os corpos são atraídos pelo planeta através da força peso (P) que lhes imprime uma aceleração de aproximadamente 10m/s² (que é constante), conhecida como aceleração da gravidade (g).
Análise Algébrica do MUV
Quando iniciamos a observação de um movimento acelerado, em t0=0 o móvel tem uma velocidade inicial v0, e em outro instante t, uma velocidade final v. Como já estudamos, a intensidade da aceleração (tangencial) média é dada, por:
Função Horária da Velocidade
Como o valor da aceleração a é constante, e a velocidade inicial v0 é conhecida, podemos arrumar a equação acima, colocando o valor final da velocidade v, em função do tempo t:
Por exemplo, imagine um móvel que ao iniciarmos a sua observação (t0) tenha uma velocidade inicial v0=20m/s, e sabemos ainda que sua aceleração é constante e tem intensidade a=5m/s². A função que nos permite determinar o valor da velocidade v que o móvel terá em função do tempo t, será:
Poderíamos perguntar, qual a intensidade da velocidade v em t=7s, mantida a aceleração constante?
Basta substituir t por 7 na equação acima:
Poderíamos perguntar ainda, em que instante t o móvel alcançará uma velocidade v=60m/s?
Agora substituímos v por 60:
Sinais da velocidade e da aceleração
Os sinais das intensidades da velocidade (v) e da aceleração (a) dependem dos sentidos desses vetores em relação à orientação da trajetória:
Quando a velocidade e a aceleração têm o mesmo sinal, o módulo da velocidade aumenta com o tempo, e o movimento é chamado de acelerado.
Quando a velocidade e a aceleração têm sinais opostos , o módulo da velocidade diminui com o tempo, e o movimento é chamado de retardado.
Exemplo 1
No instante t0=0 um móvel tem velocidade de módulo 30m/s e segue no sentido oposto à orientação da trajetória. Sabe-se que sua aceleração é constante, tem módulo de 5m/s² e mesmo sentido da orientação da trajetória.
a) Determine a função horária da velocidade do móvel.
b) Determine o instante em que o móvel muda de sentido.
c) Classifique o movimento entre t0=0 e t=10s.
Resolução:
a) Módulo de um vetor corresponde ao valor absoluto da sua intensidade, mas como a velocidade tem sentido oposto ao da orientação da trajetória, significa que a velocidade inicial é negativa, ou seja, v0=-30m/s. Como a aceleração tem o mesmo sentido da orientação da trajetória, sua intensidade realmente é positiva, ou seja, a=5m/s².
Como o enunciado afirma que a aceleração é constante, o movimento é uniformemente variado (MUV). Então, a forma geral da função horária da velocidade, é:
b) A velocidade diminui, em módulo, 5m/s a cada segundo, até parar após 6s:
É nesse momento (t=6s), que, instantaneamente, a velocidade é nula (v=0) e o móvel muda de sentido, passando a retornar aumentando a velocidade 5m/s a cada segundo:
Mas é possível conhecer o instante t em que o móvel muda de sentido a partir da função horária da velocidade, sabendo que isso acontece quando o móvel pára instantaneamente, ou seja, quando v=0:
c) A aceleração é constante, então o movimento é uniformemente variado, mas entre 0 e t=6s, a velocidade é negativa (movimento retrógrado) e a aceleração é positiva (movimento retardado, já que velocidade e aceleração têm sinais opostos). Assim, a classificação nesse intervalo de tempo é movimento uniformemente retardado e retrógrado.
Após 6s, a velocidade passa a ser positiva (movimento progressivo) como a aceleração (movimento acelerado, já que velocidade e aceleração têm o mesmo sinal). Então a classificação após t=6s é movimento uniformemente acelerado e progressivo.
Gráfico v x t
A função horária da velocidade é uma função polinomial do 1o grau, ou seja, uma função linear.
Perceba que o coeficiente angular da reta é a aceleração a. Quanto maior o módulo da aceleração, mais inclinada é a reta que representa o gráfico v x t.
Se a aceleração for positiva, o gráfico é crescente:
Se a aceleração for negativa, o gráfico é decrescente:
Exemplo 2
O gráfico abaixo mostra como a intensidade da velocidade v de um móvel varia em função do tempo t. Sabe-se que sua aceleração é constante.
a) Determine a intensidade da aceleração.
b) Qual a função horária da velocidade?
c) Em que instante o móvel muda de sentido?
d) Classifique o movimento.
e) Que distância o móvel percorre entre t=0 e t=16s?
Resolução:
a) Como a aceleração é constante, podemos usar qualquer variação de velocidade em determinado intervalo de tempo para conhecermos a sua intensidade. Em t=10s, v=0:
Uma outra forma possível, e equivalente, é partir da forma geral da função horária da velocidade:
b) Então, a função horária da velocidade é:
c) Como já vimos, o móvel muda de sentido quando pára instantaneamente, ou seja, quando v=0. O próprio gráfico já nos mostra que isso acontece em t=10s.
Mas é possível usar a função horária da velocidade, embora seja redundante:
d)
e) A área entre o gráfico e o eixo do tempo nos gráficos v x t representa a distância percorrida. Se a área estiver acima da linha do tempo, ela é positiva (deslocamento a favor da trajetória), se a área estiver abaixo da linha do tempo, ela é negativa (deslocamento contrário à orientação da trajetória).
Em t=16s:
Assim:
Então, entre t=0 e t=16s percorre uma distância:
Função Horária da Posição
Por exemplo, imagine um móvel que ao iniciarmos a sua observação (t0) tenha uma velocidade inicial v0=20m/s, e sabemos ainda que sua aceleração é constante e tem intensidade a=5m/s². A função que nos permite determinar o valor da velocidade v que o móvel terá em função do tempo t, será:
Poderíamos perguntar, qual a intensidade da velocidade v em t=7s, mantida a aceleração constante?
Basta substituir t por 7 na equação acima:
Poderíamos perguntar ainda, em que instante t o móvel alcançará uma velocidade v=60m/s?
Agora substituímos v por 60:
Sinais da velocidade e da aceleração
Os sinais das intensidades da velocidade (v) e da aceleração (a) dependem dos sentidos desses vetores em relação à orientação da trajetória:
Quando a velocidade e a aceleração têm o mesmo sinal, o módulo da velocidade aumenta com o tempo, e o movimento é chamado de acelerado.
Quando a velocidade e a aceleração têm sinais opostos , o módulo da velocidade diminui com o tempo, e o movimento é chamado de retardado.
Exemplo 1
No instante t0=0 um móvel tem velocidade de módulo 30m/s e segue no sentido oposto à orientação da trajetória. Sabe-se que sua aceleração é constante, tem módulo de 5m/s² e mesmo sentido da orientação da trajetória.
a) Determine a função horária da velocidade do móvel.
b) Determine o instante em que o móvel muda de sentido.
c) Classifique o movimento entre t0=0 e t=10s.
Resolução:
a) Módulo de um vetor corresponde ao valor absoluto da sua intensidade, mas como a velocidade tem sentido oposto ao da orientação da trajetória, significa que a velocidade inicial é negativa, ou seja, v0=-30m/s. Como a aceleração tem o mesmo sentido da orientação da trajetória, sua intensidade realmente é positiva, ou seja, a=5m/s².
Como o enunciado afirma que a aceleração é constante, o movimento é uniformemente variado (MUV). Então, a forma geral da função horária da velocidade, é:
b) A velocidade diminui, em módulo, 5m/s a cada segundo, até parar após 6s:
É nesse momento (t=6s), que, instantaneamente, a velocidade é nula (v=0) e o móvel muda de sentido, passando a retornar aumentando a velocidade 5m/s a cada segundo:
Mas é possível conhecer o instante t em que o móvel muda de sentido a partir da função horária da velocidade, sabendo que isso acontece quando o móvel pára instantaneamente, ou seja, quando v=0:
c) A aceleração é constante, então o movimento é uniformemente variado, mas entre 0 e t=6s, a velocidade é negativa (movimento retrógrado) e a aceleração é positiva (movimento retardado, já que velocidade e aceleração têm sinais opostos). Assim, a classificação nesse intervalo de tempo é movimento uniformemente retardado e retrógrado.
Após 6s, a velocidade passa a ser positiva (movimento progressivo) como a aceleração (movimento acelerado, já que velocidade e aceleração têm o mesmo sinal). Então a classificação após t=6s é movimento uniformemente acelerado e progressivo.
Gráfico v x t
A função horária da velocidade é uma função polinomial do 1o grau, ou seja, uma função linear.
Perceba que o coeficiente angular da reta é a aceleração a. Quanto maior o módulo da aceleração, mais inclinada é a reta que representa o gráfico v x t.
Se a aceleração for positiva, o gráfico é crescente:
Se a aceleração for negativa, o gráfico é decrescente:
Exemplo 2
O gráfico abaixo mostra como a intensidade da velocidade v de um móvel varia em função do tempo t. Sabe-se que sua aceleração é constante.
a) Determine a intensidade da aceleração.
b) Qual a função horária da velocidade?
c) Em que instante o móvel muda de sentido?
d) Classifique o movimento.
e) Que distância o móvel percorre entre t=0 e t=16s?
Resolução:
a) Como a aceleração é constante, podemos usar qualquer variação de velocidade em determinado intervalo de tempo para conhecermos a sua intensidade. Em t=10s, v=0:
Uma outra forma possível, e equivalente, é partir da forma geral da função horária da velocidade:
c) Como já vimos, o móvel muda de sentido quando pára instantaneamente, ou seja, quando v=0. O próprio gráfico já nos mostra que isso acontece em t=10s.
Mas é possível usar a função horária da velocidade, embora seja redundante:
d)
e) A área entre o gráfico e o eixo do tempo nos gráficos v x t representa a distância percorrida. Se a área estiver acima da linha do tempo, ela é positiva (deslocamento a favor da trajetória), se a área estiver abaixo da linha do tempo, ela é negativa (deslocamento contrário à orientação da trajetória).
Em t=16s:
Assim:
Então, entre t=0 e t=16s percorre uma distância:
Função Horária da Posição
No instante (t=0) em que começamos a observar um móvel em MUV, com aceleração constante de intensidade a, ele estará passando por uma posição inicial s0, com uma velocidade inicial v0.
Suponha que a aceleração a e a velocidade inicial v0 sejam positivas (a>0, v0>0). O gráfico v x t seria, assim:
Já vimos que a velocidade média vm é determinada, assim:
Onde Δs é a distância percorrida no intervalo de tempo Δt=t (t0=0).
Mas, Δs no gráfico v x t corresponde a área sobre o eixo do tempo:
Perceba que a figura é um trapézio (deitado), cuja área corresponde à soma da base maior (v) com a base menor (v0), multiplicada pela altura (t), e tudo dividido por 2:
Aplicando este resultado na definição da velocidade média, teremos:
O MUV é o único movimento cuja velocidade média é também a média das velocidades. Repito, esse resultado só é válido para o MUV.
Lembre-se que Δs corresponde à diferença entre a posição final (s) e a posição inicial (s0):
Lembre-se que a velocidade final v é dada, por:
Então, vamos retornar à definição de velocidade média e fazer o seguinte:
Isolando a posição final (s), teremos:
A equação acima é chamada de função horária da posição (ou espaço).
Gráfico s x t
A função horária da posição é uma função polinomial do 2o grau. Os gráficos s x t são parábolas.
A aceleração a, que acompanha t², determinará se a parábola tem concavidade voltada para cima (se a for positiva), ou para baixo (se a for negativa).
Vamos dar um exemplo. Imagine um móvel em que, ao iniciarmos a observação do seu movimento (MUV) no instante t=0 estivesse passando pela posição s0= 80m, com uma velocidade v0=20m/s, com uma aceleração constante, de intensidade a=-6m/s².
A sua função horária da velocidade, é:
E, a função horária da posição, é:
➤A parábola do gráfico s x t é voltada para baixo, já que a aceleração é negativa (a<0 font="">
➤A parábola corta o eixo das posições (s), em s0 (termo independente).
➤A parábola corta o eixo horizontal (do tempo) nas raízes da função. Ou seja, nos instantes em que o móvel passa pela origem das posições (s=0).
Perceba que na matemática usamos normalmente para o eixo horizontal (abscissas) a variável x, e na vertical (as ordenadas), a variável y.
No MUV, a horizontal é o tempo t, e a vertical é a posição s. Você precisa associar o que você estudou na matemática com as grandezas físicas envolvidas no movimento.
➤O topo da parábola está situado no instante t em que o móvel muda de sentido, ou seja, onde (instantaneamente) a velocidade é nula (v=0). Poderíamos usar o que aprendemos na matemática sobre as coordenadas do vértice para determinarmos este instante, mas podemos usar a função horária da velocidade para isso:
Conhecido este instante, podemos aplicá-lo na função horária da posição para determinar em que posição (s) ele pára instantaneamente:
Com estas informações, o gráfico s x t, para este movimento, ficaria assim:
Perceba que o que aconteceu ANTES de iniciarmos a observação do movimento não nos interessa, porque não estávamos vendo o que ocorria.
Exemplo 3
Um móvel parte do repouso e acelera de forma constante a=2,0 m/s².
a) Qual o módulo da sua velocidade após 3,0s?
b) Que distância percorrerá nesse intervalo de tempo?
Resolução:
a) A função horária da velocidade para o móvel, é:
Então, em t=3,0s, sua velocidade será:
b) Como nada foi dito sobre a posição inicial, podemos dizer que o móvel partiu da origem das posições, ou seja, s0=0. Desse modo, a função horária da posição será:
Então, em t=3,0s, ele estará na posição:
Como consideramos que partiu de s0=0, significa que em 3,0s percorreu 9,0m de distância.
Exemplo 4
Uma partícula em movimento retilíneo, movimenta-se de acordo com a equação v=10+3t, com o espaço em metros (m) e o tempo em segundos (s). Sabe-se que em t=0 passava pela posição s0=-30m.
Suponha que a aceleração a e a velocidade inicial v0 sejam positivas (a>0, v0>0). O gráfico v x t seria, assim:
Onde Δs é a distância percorrida no intervalo de tempo Δt=t (t0=0).
Mas, Δs no gráfico v x t corresponde a área sobre o eixo do tempo:
Perceba que a figura é um trapézio (deitado), cuja área corresponde à soma da base maior (v) com a base menor (v0), multiplicada pela altura (t), e tudo dividido por 2:
Aplicando este resultado na definição da velocidade média, teremos:
O MUV é o único movimento cuja velocidade média é também a média das velocidades. Repito, esse resultado só é válido para o MUV.
Lembre-se que Δs corresponde à diferença entre a posição final (s) e a posição inicial (s0):
Lembre-se que a velocidade final v é dada, por:
Então, vamos retornar à definição de velocidade média e fazer o seguinte:
Isolando a posição final (s), teremos:
A equação acima é chamada de função horária da posição (ou espaço).
Gráfico s x t
A função horária da posição é uma função polinomial do 2o grau. Os gráficos s x t são parábolas.
A aceleração a, que acompanha t², determinará se a parábola tem concavidade voltada para cima (se a for positiva), ou para baixo (se a for negativa).
Vamos dar um exemplo. Imagine um móvel em que, ao iniciarmos a observação do seu movimento (MUV) no instante t=0 estivesse passando pela posição s0= 80m, com uma velocidade v0=20m/s, com uma aceleração constante, de intensidade a=-6m/s².
A sua função horária da velocidade, é:
E, a função horária da posição, é:
➤A parábola do gráfico s x t é voltada para baixo, já que a aceleração é negativa (a<0 font="">
➤A parábola corta o eixo das posições (s), em s0 (termo independente).
➤A parábola corta o eixo horizontal (do tempo) nas raízes da função. Ou seja, nos instantes em que o móvel passa pela origem das posições (s=0).
Perceba que na matemática usamos normalmente para o eixo horizontal (abscissas) a variável x, e na vertical (as ordenadas), a variável y.
No MUV, a horizontal é o tempo t, e a vertical é a posição s. Você precisa associar o que você estudou na matemática com as grandezas físicas envolvidas no movimento.
➤O topo da parábola está situado no instante t em que o móvel muda de sentido, ou seja, onde (instantaneamente) a velocidade é nula (v=0). Poderíamos usar o que aprendemos na matemática sobre as coordenadas do vértice para determinarmos este instante, mas podemos usar a função horária da velocidade para isso:
Conhecido este instante, podemos aplicá-lo na função horária da posição para determinar em que posição (s) ele pára instantaneamente:
Com estas informações, o gráfico s x t, para este movimento, ficaria assim:
Perceba que o que aconteceu ANTES de iniciarmos a observação do movimento não nos interessa, porque não estávamos vendo o que ocorria.
Exemplo 3
Um móvel parte do repouso e acelera de forma constante a=2,0 m/s².
a) Qual o módulo da sua velocidade após 3,0s?
b) Que distância percorrerá nesse intervalo de tempo?
Resolução:
a) A função horária da velocidade para o móvel, é:
Então, em t=3,0s, sua velocidade será:
b) Como nada foi dito sobre a posição inicial, podemos dizer que o móvel partiu da origem das posições, ou seja, s0=0. Desse modo, a função horária da posição será:
Então, em t=3,0s, ele estará na posição:
Como consideramos que partiu de s0=0, significa que em 3,0s percorreu 9,0m de distância.
Exemplo 4
Uma partícula em movimento retilíneo, movimenta-se de acordo com a equação v=10+3t, com o espaço em metros (m) e o tempo em segundos (s). Sabe-se que em t=0 passava pela posição s0=-30m.
Determine para essa partícula:
a) A velocidade inicial.
b) A sua velocidade em t=4,0s.
c) A sua aceleração em t=4,0s.
a) A velocidade inicial.
b) A sua velocidade em t=4,0s.
c) A sua aceleração em t=4,0s.
d) A sua função horária da posição.
e) A distância percorrida até o instante instante t=4,0s.
Resolução:
a) A função horária da velocidade v=10+3t (linear) mostra que o movimento é uniformemente variado (MUV), onde:
Então, a velocidade inicial é 10m/s.
b)
e) No instante t=4,0s, a partícula estará na posição:
Mas:
Então, terá percorrido uma distância de 64m nesse intervalo de tempo.
a) A função horária da velocidade v=10+3t (linear) mostra que o movimento é uniformemente variado (MUV), onde:
Então, a velocidade inicial é 10m/s.
b)
Em t=4,0s, a velocidade será de 22m/s.
c) Como o movimento é uniformemente variado, significa que sua aceleração é constante. Logo, em qualquer instante terá sempre a mesma direção e intensidade. Assim, a intensidade da aceleração em t=4,0s será a=3m/s².
d)
Então, terá percorrido uma distância de 64m nesse intervalo de tempo.